[算法]-搜索-AVL、红黑树

发表于 | 分类于 | 阅读次数

二叉查找树最坏情况下的时间和树的高度成正比（O(n)），所以当最坏情况的性能还是很糟糕，所以我们可以用AVL、红黑树等数据结构，能保证无论如何构造他她的运行时间都是对数级（树的高度是LogN）

平衡二叉树（AVL）

定义：
父节点的左子树和右子树的高度之差不能大于1，也就是说不能高过1层，否则该树就失衡了，此时就要旋转节点，在编码时，我们可以记录当前节点的高度，比如空节点是-1，叶子节点是0，非叶子节点的height往根节点递增。

为了保证这一点，在树出现失衡时(左右子树高度相差大于1)需要进行旋转（调整树的高度）操作。

失衡有四种情况：

左左 LL 左旋转

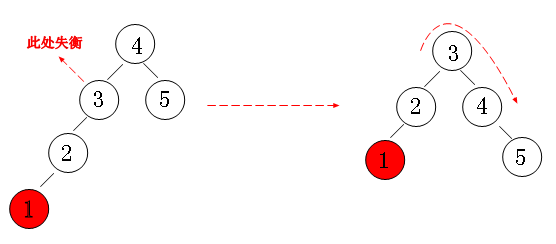
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
/**
    * @Author jiaxuehui
    * @Description 左旋转,root2变成根节点，root2的右子树变成root1的左子树，root1变成root2的右子树
    * @Date 8:47 PM 08/11/2018
    * @Param root1 失衡的子树跟节点
    * @return root2 旋转之后的新根节点
    *
    **/
private AVLnode LL(AVLnode root1){
       AVLnode root2 = root1.left;
       root1.left = root2.right;
       root2.right = root1;
       //重新计算高度
       root1.height = Math.max(height(root1.left), height(root1.right))+1;
       root2.height = Math.max(height(root1.left), root2.height)+1;
       return root2;
   }

右右 RR 右旋转

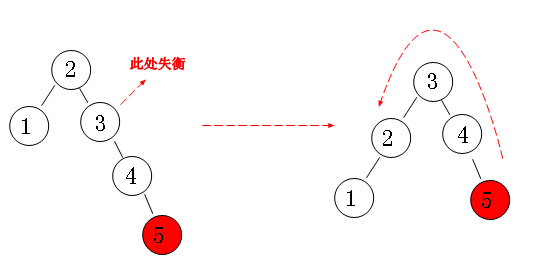
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
/**
   * @Author jiaxuehui
   * @Description 右旋转
   * @Date 9:01 PM 08/11/2018
   * @Param  @Param root1 失衡的节点
   * @return root2 旋转之后的新根节点
   *
   **/

  private AVLnode RR(AVLnode root1){
      AVLnode root2 = root1.right;
      root1.right = root2.left;
      root2.left = root1;

      root1.height = Math.max(height(root1.left), height(root1.right))+1;
      root2.height = Math.max(height(root1.right), root2.height)+1;
      return root2;
  }

左右 LR 先左旋转再右旋转

1
2
3
4
5
6
7
8
9
10
11
12
13
14
 
/**
 * @Author jiaxuehui
 * @Description 左右旋转， 该节点的左子树进行右旋转，再对该节点进行左旋转
 * @Date 9:05 PM 08/11/2018
 * @Param root1 失衡的节点
 * @return
 *
 **/

private AVLnode LR(AVLnode root1){
    RR(root1.left);
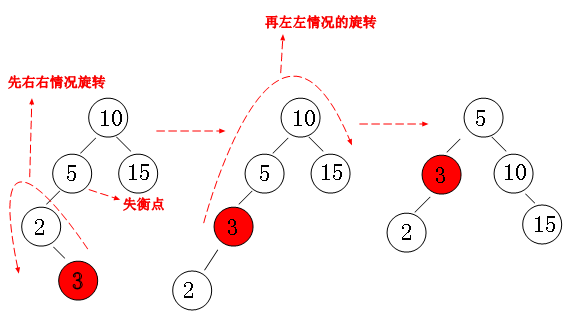
    return LL(root1);
}

右左 RL 先右旋转再左旋转

1
2
3
4
5
6
7
8
9
10
11
12
13
/**
  * @Author jiaxuehui
  * @Description 右左旋转， 该节点的右子树进行左旋转，再对该节点进行右旋转
  * @Date 9:05 PM 08/11/2018
  * @Param root1 失衡的节点
  * @return
  *
  **/

 private AVLnode RL(AVLnode root1){
     RR(root1.right);
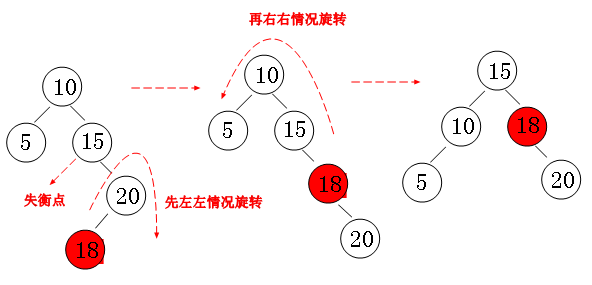
     return LL(root1);
 }

获取节点高度的方法：

1
2
3
4
5
6
7
 public int height(){  //节点高度是子树最高的高度加1
    return root.height;
}

public int height(AVLnode root){  //为了递归计算树的高度
    return height(root);
}

每次插入节点之后，判断一下如果节点失衡，就进行相应的旋转

红黑树

什么是红黑树

红黑树是一个自平衡树，它没有AVL那么平衡，它不追求完全平衡，而是最长路径不大于最短路径的二倍（所有路径黑色节点数相同，不能有连续的红色），这样降低了对，转的要求，提升了性能。

构造红黑树需要满足以下几个原则，这些限制保证了树的自平衡。

  1. 节点是红色或黑色。

  2. 根节点是黑色。

  3. 每个叶子节点都是黑色的空节点（NIL节点）–叶子节点是红色。

  4. 每个红色节点的两个子节点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色节点，黑色可以连续)

  5. 从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。

根据规则5，我们知道如果红黑没跳路径有N个黑色节点，树可能的最短的路径是N，即全部都是黑色节点，高度为N-1，可能的最长路径是红黑相间，高度为2（N-1）

如下一棵红黑树：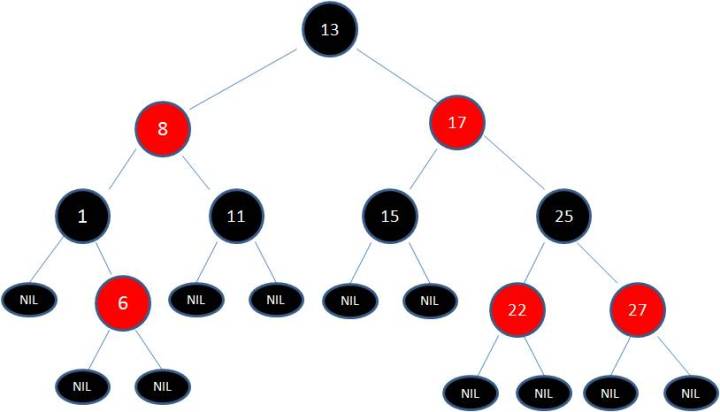

调整红黑树的结构

在添加和删除节点的时候红黑树的平衡可能会被打破，需要做出一些调整（变色，旋转）来保持平衡。

当我们插入节点的时候，将要插入的节点着色为红色，因为着色会红色只有一半几率破坏规则4，而着黑色则一定会破坏规则5，且规则4比规则5更好修正。

所以插入一个节点时，我们先判断是否违反了规则4，如果是，则用变色的过程将树变色到满足规则.如果这时变色解决不了问题的话（不能同时满足5个规则），则可能需要一些列的旋转（来转移黑色节点的位置）、变色来保证满足原则。

情况1：插入到两个黑色节点之间

不破坏规则，插入结束

情况2: 父节点是红色，叔叔节点也是红色

这种情况由于根节点的两个孩子是一样的颜色，所以变色后两个子树的黑色节点数仍然相同。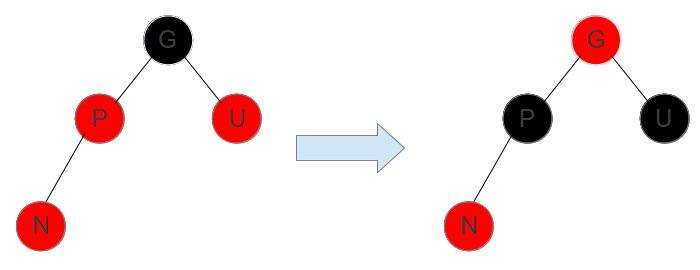

N是新加入的节点，这种情况我们把P涂成黑色，G涂成红色，U涂成红色。重新满足规则，每条路径上的黑色节点数没有变化。

但是如果G的父节点也是红色的话，需要继续重复上述过程往上变色直至父节点是个黑色节点。

情况3: 父节点是红色，叔叔节点是黑色


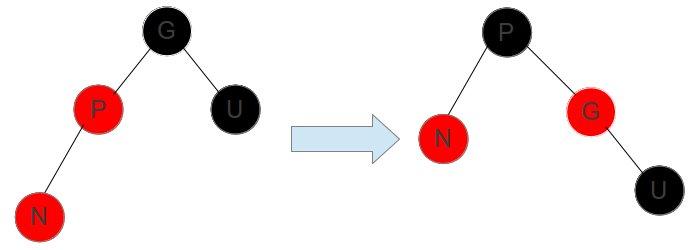
这种情况如果按上述方案变化，两棵子树的黑色节点数就不同了，为了转移黑色节点使其仍然满足规则五，则需要进行一次旋转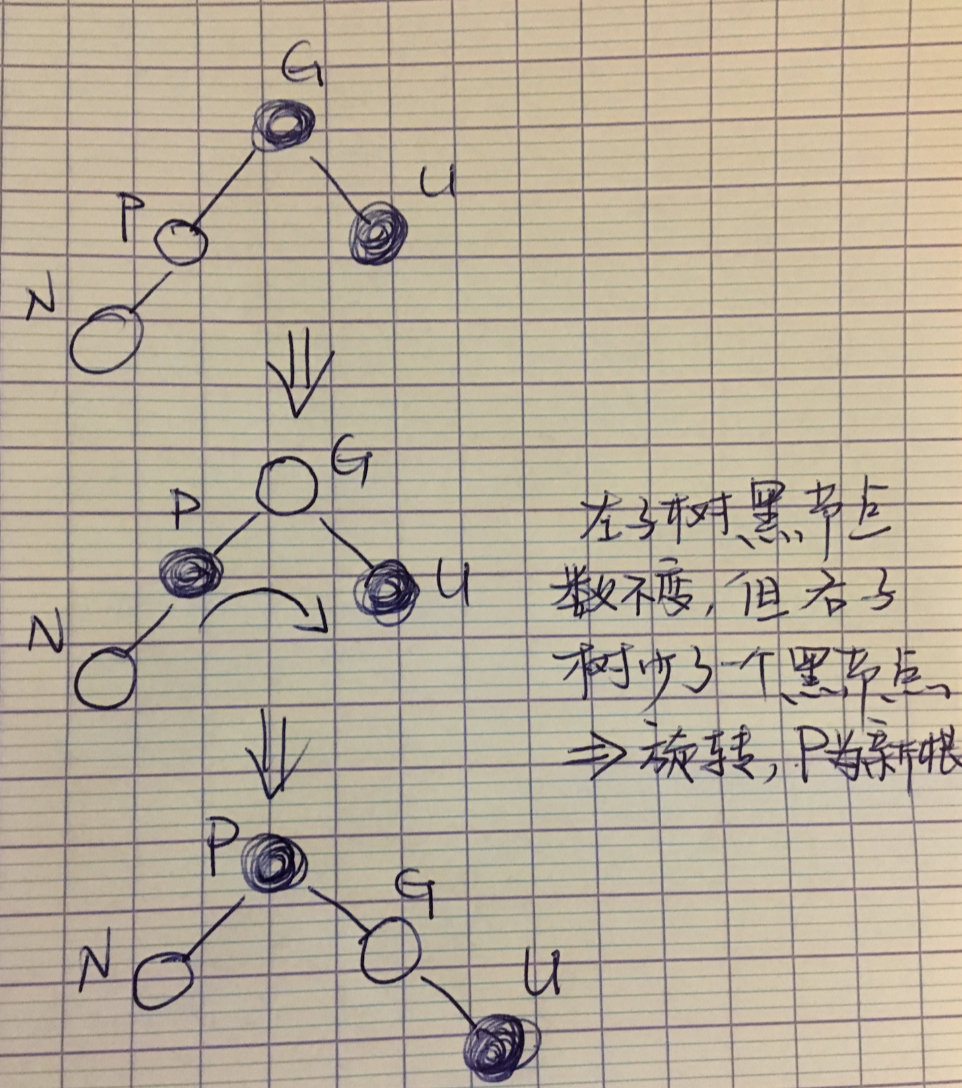

一个例子：http://lvshen9.coding.me/2017/11/07/红黑树的变色与旋转/

AVL和红黑树对比


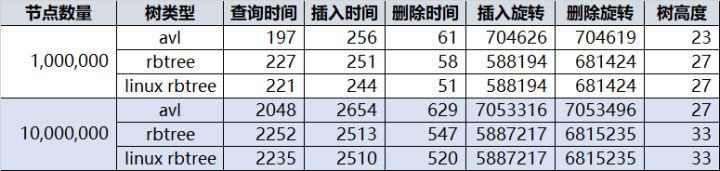
AVL和红黑树的时间复杂度相同，但是红黑树的统计性能比AVL更高。

查询时间

AVL优于红黑树，因为红黑树不是绝对的平衡，树的高度大于AVL。而查询的复杂度主要取决于书的高度。两者都是O（logN）

插入和删除

红黑树优于AVL，因为红黑树不追求绝对平衡，由于他的设计，任何不平更都会在三次旋转之内解决。红黑树旋转次数更少。两者都是O（logN）